날짜는 의미 없으므로 앞으로 제목에 날짜를 안적기로한다. 의미가 있는건 내가 오늘 뭘 배우고 뭘 이해했는지 기록을 위한거라 생각한다.
원-핫인코딩 (One - hot encoding)
인간과 컴퓨터는 데이터를 바라보는 형태가 다르기 때문에 이를 번역(?)하는 과정이 필요하다.
컴퓨터는 모든 데이터를 숫자를 바탕으로 이해하기에 컴퓨터가 문자를 이해할 수 있는 숫자로 바꾸며 이러한 결과를 임베딩이라고 한다.
원-핫 인코딩은 수많은 데이터를 0과 한개의 1의 값으로 데이터를 구별하는 인코딩이다.
표현하고자 하는 인덱스에 1, 다른 인덱스에는 0을 부여하는 벡터 표현방식이며 이렇게 표하는 것을 원-핫 백터라고 부른다고 한다.
범주형(Catagorical) 자료를 다루기 위하여 사용한다.
범주형 자료란 ?
명목형 자료(nomianl data)와 순서형 자료(ordinal data)로 나뉘며
단순히 성별 ,성공여부,혈액형과 같은 경우에는 단순히 분류를 목적으로 하는 명목형 자료라고 하며
쎄다 보통이다 약하다와 같이 순서에 의미가 있는 자료를 순서형 자료라 한다. 순서형 자료는 원핫인코딩으로 하기 어려운지
배우지 않았다.
릿지회귀 (Ridge Regression)
다중 선형 회귀 모델은 특성이 많아질수록 훈련 데이터에 과적합 되기 쉽다.
과적합된 다중 선형 회귀 모델은 단 하나의 특이값에도 회귀선의 기울기가 크게 변할 수 있는데
릿지 회귀는 어떤 값을 통해 이 기울기가 덜 민감하게 반응하게 끔 만들며 이 값을 람다(lamda 𝜆)라고 한다.
릿지 회귀를 어떻게, 왜 쓸까?
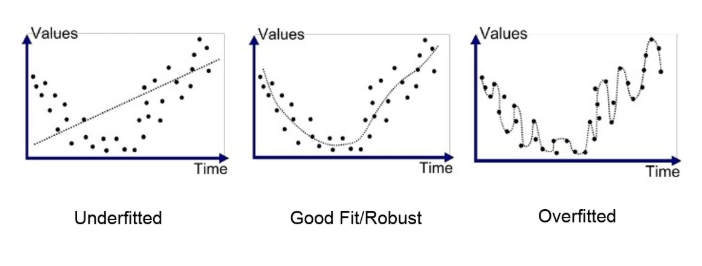
첫번째 그림을 보면 직선 방정식을 이용하여 선이 그어진것을 볼 수 있고 데이터(점)과 직선의 모양이 꽤나 차이가 나는 것을
볼 수가 있다. 이러한 경우를 과소적합(Underfitted), 높은 편향(High bias) 상태라고 한다.
과소적합의 경우 기계 학습에서 통계 모형의 능력 부족으로 학습 데이터를 충분하게 설명치 못하도록 부족하게 학습된 것을 의미한다.
즉 test data를 위한 학습이 덜 된 것이 원인으로 저러한 모양이 나온다는 것이다.
세번째 그림을 보면 주어진 데이터(점)은 정확하게 잘 맞아 떨어지지만 이 경우가 아닌 다른 데이터를 사용한다면 정확한 예측을 하지 못하게 된다. 이러한 경우를 과대적합(Overfitting) 또는 높은 분산(high variance) 상태라고 한다.
과대적합의 경우 머신러닝 모델을 학습 할 때 학습 데이터셋에 지나치게 최적화 되었다는 의미이다.
두번째 그림은 최적화가 잘 된 그림이라고 볼 수 있는데, 모델을 만들 때 overfitting을 해결하게 되면 가운데의 모양을 갖출 수 있다.
과대적합을 해결하는데에는 크게 두가지 방법이 있다고 한다.
1. 특성을 선택한다(Feature selection)
- SeletionKbest, Model selection algorithm 등
- 주요 특징을 직접 선택하고 나머지는 버린다.
2. 정규화를 수행한다.(Regularization)
- 모든 특성을 사용하되, 파라미터(세타)의 값을 줄인다.
이 부분에서 과적합을 줄이기 위해 정규화 컨셉을 도입한 모델이 바로 릿지 회귀이다.

n: 샘플수, p: 특성수, 𝜆: 튜닝 파라미터(패널티) 참고: alpha, lambda, regularization parameter, penalty term 모두 같다.
릿지 회귀는 편향을 조금 더하고 분산을 줄이는 방법으로 정규화를 수행한다.
릿지 회귀 식을 보면 잔차제곱합(Rss:residual sum of squares) + 페널티 항(베타 값)의 합으로 이루어져잇다.
릿지회귀의 페널티항은 파라미터의 제곱을 더해준 것이다.
람다(𝜆) 값의 조정(기울기의 조정)을 통해 페널티를 얼마나 부과하는지 정한다.
만약 람다가 0이라면 위 식으 다중 선형 회귀와 동일해지며
반대로 람다가 커지면 커질수록 다중 회귀선의 기울기를 떨어뜨려 0으로 수렴하게 만드는데 이는 덜 중요한 특성의 개수를
줄이는 효과로 볼 수 있다.
데이터셋을 분리 해야하는 이유 (test, train)
- 과적합인지 과소적합인지 판단하기 위해 곂치지 않는 데이터로 테스트를 해야한다
다중선형회귀
회귀 평가지표 : mae, mse, rmse, r2 등..
과적합 / 과소적합
분산이 클 때 -> 과적합 큰 상태
편향이 클 때 -> 과소적합이 큰 상태
어떻게 분산을 감소 시킬까?
분산이 큰 모델이란 ? = 복잡한 모델
분산을 줄이려면? -> 단순화 , 피쳐를 줄인다, 편향을 만든다, 단순한 모델을 쓰자
머신러닝 프로젝트 프로세스
문제 정의 - 매출이 안 나온다 -> 매출을 올리자
데이터 선정 -점포별 일별 매출 데이터
데이터 분리
데이터 전처리 - EDA - Feature engineering -EDA
= 데이터 확인, 이상치 , 결측치 등 처리, 표준화 인코딩
모델링 - 선형회귀, 릿지회귀, ...
검증 - test set(평가지표를 이용)
최종 모델
모델 해석
인사이트 도출
문제 해결 솔루션 도출
'AI > 머신러닝' 카테고리의 다른 글
| 결정트리(Decision Tree) 이란? (0) | 2022.03.02 |
|---|---|
| 로지스틱 회귀 (Logistic Regression) (0) | 2022.02.25 |
| 머신러닝에서 훈련/검증/테스트 세트로 나누는 이유 (0) | 2022.02.25 |
| 단순선형회귀모델, 회귀계수 ,사이킷런 (0) | 2022.02.22 |
| 부트캠프에 관한 불만 (0) | 2022.02.22 |




댓글