728x90
경사하강법(Gradient Descent)이란 무엇일까?
- 신경망의 학습을 위해선 손실을 줄여나가야 하는데 이때 손실함수 J가 함수의 미분값을 계산하고 있을때 기울기가 완만해질수 있도록 (즉 경사가 낮아지는) 가중치를 변경하는 방법이다.
- 간단하게 말해 함수의 기울기를 이용하여 함수 값이 낮아지는 방향으로 독립 변수의 값을 변형시켜가면서 최종적으로 최소 함수 값을 갖도록 하는 독립 변수의 값을 찾는 방법이다.
- 좋은 예시로 시야가 안보일때 산에서 내려오기 위하여 산의 기울기를 더듬으며 가장 아래로 갈 수 있는 방향을 찾는 방법이 예시이다. 산에서 내려가기 위해 오르막길을 선택하지는 않을 것이기 때문이다.
*gradient를 한글로 번역하면 기울기이다.
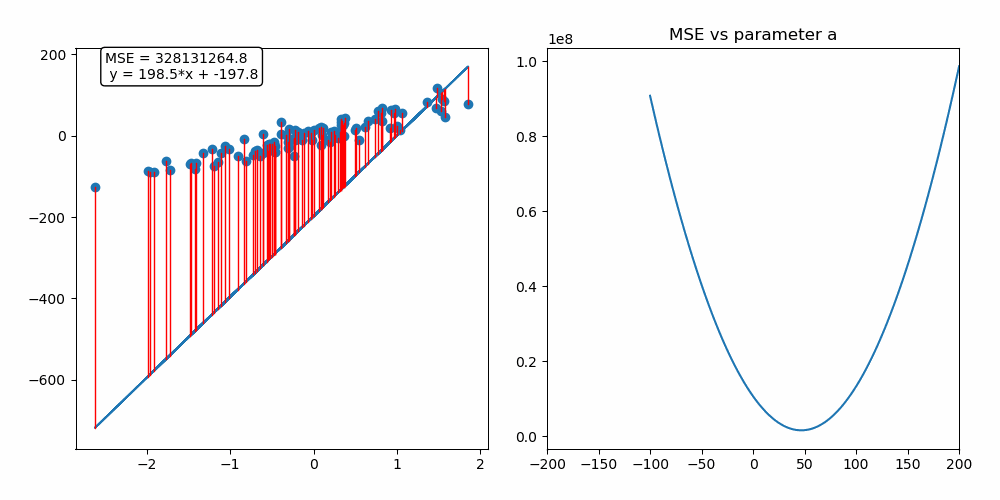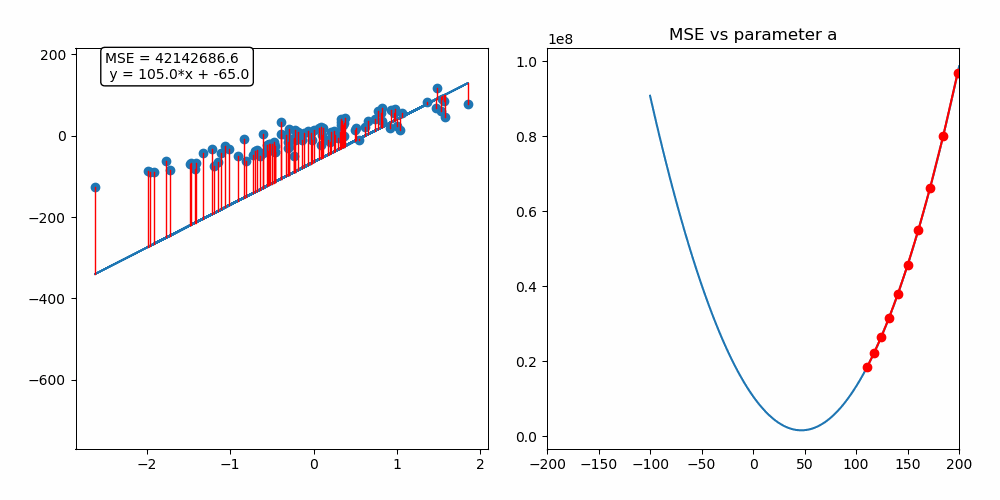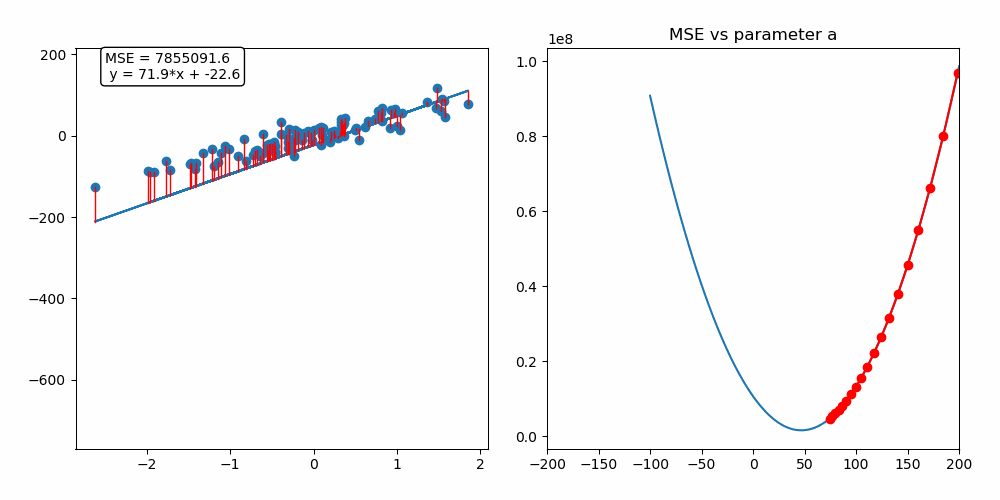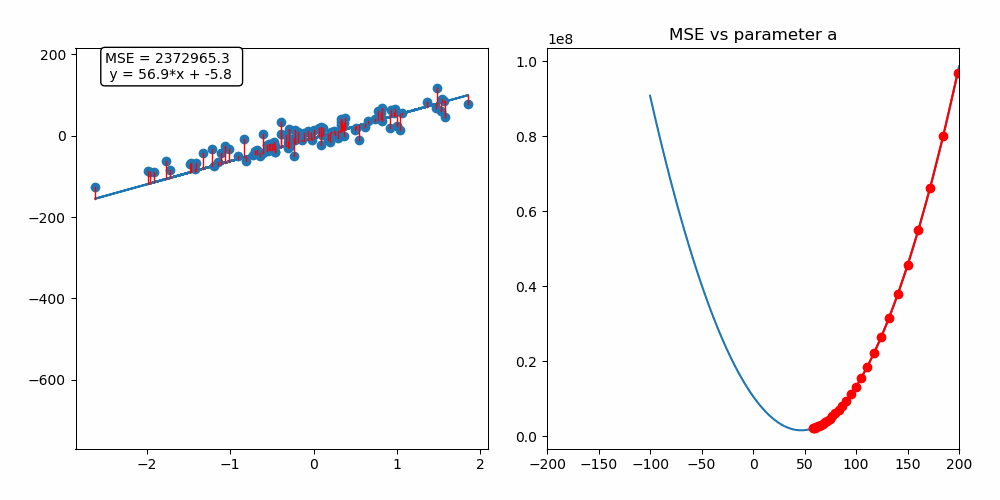
왜, 언제 경사하강법을 사용할까?
- 함수의 최솟값을 찾기 위한 문제에서 사용한다.
- 함수가 너무 복잡하여 미분 계수를 구하기 어려운 경우 사용한다.
- 데이터틔 양이 많은 경우 효율적으로 계산을 하기 위해 사용한다.
경사하강법의 원리
경사하강법은 함수의 기울기를 이용하여 X의 값을 어느 구간으로 옮겨 졌을 때 최솟값이 나오는지 찾는 방법이다.
이는 기울기가 양수라면 X값이 커질 수록 함수의 값도 커진다는 의미이고,
반대로 기울기가 음수라면 X의 값이 커질 수록 함수의 값이 작아진다는 의미이다.
이러한 원리로 기울기가 양수 일때는 X의 값을 X가 작아지는 방향으로 옮기고,
반대로 기울기가 음수인 경우에는 X가 커지는 방향으로 옮긴다면 최솟값을 찾아낼 수 있을 것이다.
즉 기울기의 부호의 반대방향으로 움직여야한다. 이때 이동거리의 경우는 최솟값에 가까워 질 수록 거리를 줄여나가야 발산하지 않기에 한다.
옵티마이저란(Optimizer)
경사하강법에서 경사를 어떻게 내려가야할지 정해주는 방법
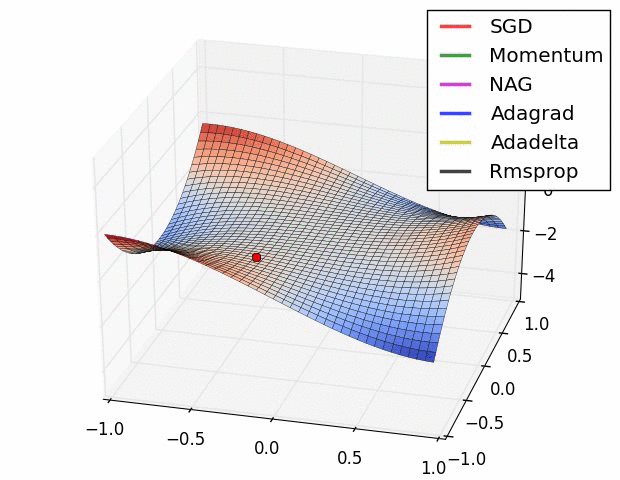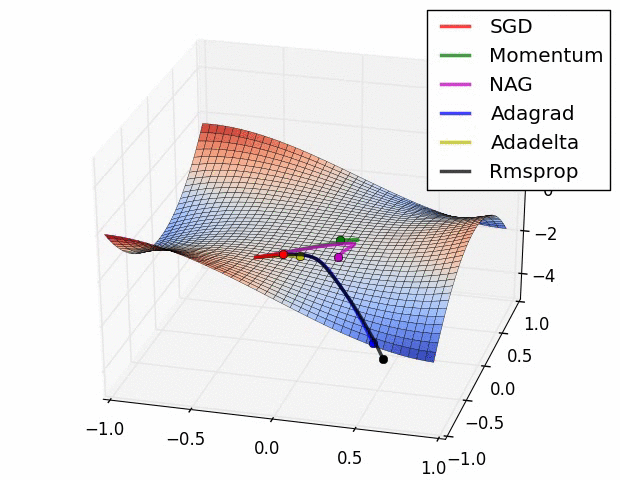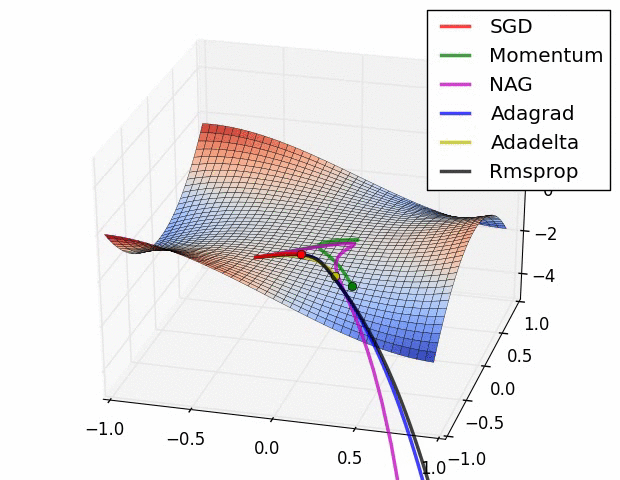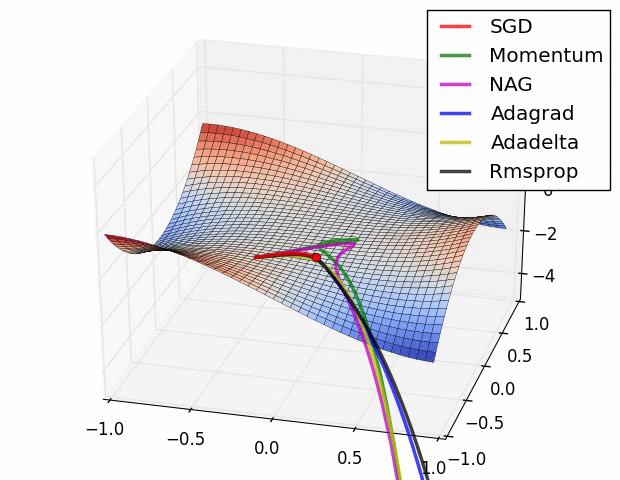
여러가지 경사하강법의 옵티마이저들중
확률적 경사하강법(Stochastic Gradient Descent, SGD)과 미니 배치 경사하강법(Mini - batch Gradient Descent)이 자주 사용되어진다고 한다.
'AI > 딥러닝' 카테고리의 다른 글
| 원-핫 인코딩(One-Hot Encoding) 이란? (0) | 2022.05.06 |
|---|---|
| 자연어 처리(Natural Language Processing)와 토큰화(tokenization)란? (0) | 2022.05.04 |
| 신경망이 학습되어지는 메커니즘(순전파,역전파,경사하강법)이란? (0) | 2022.04.29 |
| 인공 신경망(Artificial Neural Networks)이란? (0) | 2022.04.27 |
| 퍼셉트론(Perceptron)과 활성화 함수(Activation Function)란? (0) | 2022.04.27 |




댓글